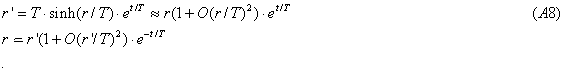On the discrepancy between optical observations of the planets and their ephemerides.

C. Johan Masreliez

1. Introduction

After the introduction of atomic time into astrometry in 1955, several investigators independently began to notice discrepancies between the planetary ephemerides and optical observations. Comparisons of optical observations with the ephemerides DE200 reduced to the FK5 stellar reference system show significant drift between the observations and the ephemeris positions (i.e. the residuals), as reported by Yao & Smith (1988, 1993), Standish & Williams (1990), Seidelman et al. (1985, 1986) and Kolesnik (1995, 1996). Furthermore, Kolesnik (2000, 2001) reports that the residuals for the innermost planets show evidence of acceleration in proportion to the planetary motions.

Conversely, ephemerides based on radar ranging measurements between the Earth and the planets and laser ranging to the Moon have not detected such accelerations (see for example Adams et. al., 1983, Williams et. Al., 1996 and 2001). The reason for this discrepancy is not known, but since it has persisted for decenniums it is unlikely that it is caused by observational errors or data reduction shortcomings.

Modern ephemerides for the inner planets primarily use radar ranging between the Earth and a planet or ranging to a spacecraft nearby a planet or landed on its surface. Laser ranging to the Moon is also used for the construction of the ephemerides. These ranging measurements are very accurate varying from a few hundreds of meters for ranging to the planets and the accuracy is improved to a few meters with the use of a transponder in a spacecraft. The accuracy is a few centimeters for lunar laser ranging (LLR). With these range measurements it has become possible to determine the ephemerides of all four inner planets and the Moon with great accuracy. This process crucially relies on the assumption that the planetary orbits may be modeled in great detail by Newton's law of gravitation taking into account its Post-Newtonian relativistic refinements. Using many independent range measurements all parameters that specify the ephemerides may be estimated. This process also automatically defines a time-base for the ephemerides as being the temporal argument, which provides the best fit to the range measurements. In this way modern ephemerides of the inner planets and the Moon primarily rely on range measurements. The time when a particular measurement is made is of secondary importance and may in principle be determined by inverse interpolation after construction of the ephemerides.

It is widely recognized that this approach of constructing ephemerides has one major disadvantage compared to optical observations - the orientation of the system of ephemerides relative to the International Celestial Reference System (ICRS) is poorly determined. However, recently it has become possible to tie the ephemerides very accurately to distant radio sources fixed in the cosmological reference frame using VLBI observations.

Another possible disadvantage of the approach is its reliance on the assumption that the planetary orbits are Post-Newtonian. However, since no systematic discrepancies from the Post-Newtonian model have been detected, the ranging observations appear to confirm that the Post-Newtonian assumption is correct. This should mean that the orientation of the dynamic reference system does not change with time. However, in spite of the very accurate ephemerides with errors in the order of one kilometer the predicted planetary positions drift relative to the ICRS and the ephemerides must be updated periodically. It is generally believed that this drift is caused by unmodeled asteroidal influences.

On the other hand, optical observations directly measure the positions of the planets relative to the stellar background and therefore automatically orient the ephemerides. As with the modern ephemerides based on ranging observations the earlier ephemerides based on optical observations were derived so that Newton's law is satisfied for the planetary motions. In the past this determined a time-base called "ephemeris time" as being the temporal argument for which the planets moved in accordance with Newton's law. It is generally believed that this ephemeris time for the older "optical ephemerides" and the time-base for the modern "ranging ephemerides" are the same and that both these time-bases are proportional to atomic time.

In this paper I will challenge this belief by showing that these three time-bases might differ from each other, which might explain the noted discrepancy between the modern ephemerides and optical observations.

In the past all modeling of the planetary motions assume that the underlying spacetime is basically Minkowskian modified by local curvature due to gravitational fields generated by the Sun, planets, moons and the asteroids. However, from the cosmological redshift we know that the universe at large appears to expand. We take for granted that spacetime locally is Minkowskian, but this might not be true; there might be some small up till now undetected spacetime curvature of cosmological origin even locally in the solar system.

According to Einstein's general relativity one can always find a local Minkowskian coordinate system if spacetime is curved. If the cosmological curvature were small and if Newton's (and Einstein's) law of gravitation were to hold in this local Minkowskian system, it would be possible to construct Post-Newtonian ephemerides using these locally Minkowskian coordinates. In this coordinate system it might be impossible to detect any deviation from the Post-Newtonian ephemerides. Furthermore, if one relies on ranging measurements and if these measurements are fitted to Post-Newtonian orbits, these "Minkowskian coordinates" would be selected automatically since they are the coordinates that provide the best fit. Thus, the process of constructing ephemerides might implicitly define a Minkowskian coordinate representation that might differ from the cosmological line element.

Thus, if spacetime is cosmologically curved the local Minkowskian coordinates might deviate from the "global" cosmological coordinates. For example, it is possible that the local Minkowskian (dynamic) coordinate system might rotate relative to the ICRS causing drift of the ephemerides relative to the cosmological reference frame. Also, the temporal argument for the planetary ephemerides, which is the same as the temporal coordinate of the Minkowskian system, might differ from the temporal coordinate of the cosmological line element. If this were true one might wonder which time-base is the "right" one. Since spectral lines seem to be the same even at huge cosmological distances, we might make the assumption that atomic time represents a true cosmological time-base and look for any discrepancy between atomic time and the ephemerides time-base.

Although this scenario might appear farfetched it should not be dismissed without further investigation since it could explain the mysterious but irrefutable disagreement between optical observations and the planetary ephemerides.

All planets move in the same direction around the Sun; therefore, if there is planetary acceleration only accelerations relative to the Earth might be detected by ranging. The planetary accelerations suggested by Kolesnik, would cause drifts relative to the Earth summarized in Table I.

Table I: Predicted planetary drifts due to acceleration
	Velocity	Relative	Relative drive (km)
Planet	(km/s)	velocity	20 years	30 years
Mercury	48	17	7.2	16.2
Venus	35	4	1.6	3.6
Earth	31	0	0	0
Mars	25	-6	-2.6	-5.8

In the process of fitting the ephemerides to the ranging data these relative drifts would be reduced significantly. The resulting deviations are of the same order as the observed drifts, which would make it necessary to update the ephemerides repeatedly.

It was mentioned above that the time-base for the ephemerides are implicitly determined in the process of ephemeris construction. However, Oesterwinter and Cohen (Oesterwinter and Cohen, 1972) use atomic time as the time-base of the ephemerides for both the planets and the Moon based on optical observations 1955-1968. Extrapolating these ephemerides backward in time to 1912 they discover that atomic time deviates from traditional ephemeris time and they estimate the deviation to be about seven seconds in fifty years in good agreement with recent results by Kolesnik (Kolesnik, 2000, 2001). At least two other independent investigations estimate the relative accelerations between the planets based on radar ranging data and atomic time (Reasenberg and Shapiro, 1968 and Krasinsky et al. 1986). Both these studies also detect positive acceleration of the planets.

If the planetary accelerations were real it might seems that they should have been discovered a long time ago. At least, they should have been detected when fitting the modern ephemerides to the very precise ranging measurements. However, I will show that a coordinate representation might exist in which the ephemerides are perfectly post-Newtonian even if the planets were accelerating relative to the ICRS. With this coordinate system the temporal and radial coordinates might differ from those of a reference system based on atomic time. Therefore, the discrepancy between optical and ranging measurements methods might be explained by the use of different coordinate representations. The source of the discrepancy would then lie in the presumed post-Newtonian model rather than in any procedural, computational or observational shortcoming.

2. The effect of a curved cosmological line element.

As an example I will consider a cosmological line element earlier proposed by the author (Masreliez, 1999) according to which the universe evolves by expanding all four metrics of spacetime:

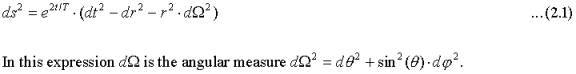
T is the Hubble time.

The corresponding geodesic equations for the radial coordinate and one of the angular coordinates are:

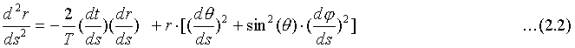
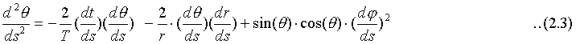
The first terms on the right hand side in these equations model a new phenomenon "cosmic drag", which reduces the linear and angular momentums of freely moving particles over time. Assuming that the temporal coordinate, t, is proportional to atomic time and that the distance, r, is the light distance timed with an atomic clock, the planets slowly spiral toward the Sun.

Masreliez (Masreliez, 1999) shows using (2.3) that this implies that the angular momentum for small velocities satisfies:

The secular acceleration (2.5) agrees excellently with Kolesnik's estimates for the three innermost planets based on optical observations if the Hubble time is about 14 billion years. (Kolesnik, 2000, 2001). Also, it agrees with the finding of Oesterwinter and Cohen since the secular acceleration of the Earth, which according to (2.5) is 2.5-3.0"/cy², would cause a difference between atomic time and ephemeris time of about seven seconds on fifty years.

Masreliez (2000) also presents a variable transformation that will transform the line element (2.1) into a line element that locally is very close to the Minkowski line element:

The corresponding equivalent line element is:

The geodesic equations for this line element corresponding to (2.2) and (2.3) are derived in the Appendix:

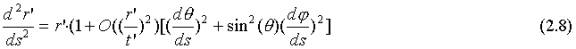
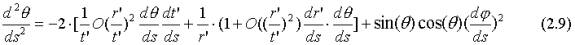
Since the temporal coordinate t^’ is close to the Hubble time T the ratio (r^’/t^’) is of the order 10^-15 in the solar system. Within the solar system the line element (2.7) can therefore be treated as being identical to that of the Minkowski spacetime, causing the cosmic drag terms in (2.2) and (2.3) to disappear. One can also show that the deviation from Newton's law of gravitation implied by the transformation (2.6) is of the order (r/T)². Thus, if the temporal and spatial coordinates were given by the equivalent line element (2.7), there would be no planetary acceleration or any other measurable deviation from the standard law of gravitation.

The relationships between the coordinates for the two line elements are derived in the Appendix:

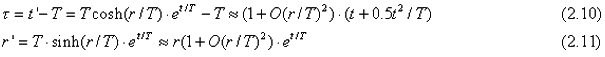
The time-base τ , which I will call the "Newtonian base", accelerates relative to atomic time with the temporal acceleration 1/T, which corresponds to about 20 seconds/century² if T=14 billion years and the "atomic distance" r decreases with time relative to the "Newtonian distance", r^’.

Nowadays all timing measurements use atomic time, t, instead of Newtonian time, τ, but the measured ranging distances due to the two different time-bases would be almost identical (the difference is less than a millimeter for the inner planets). Thus, if the ephemerides were fitted solely based on ranging data there would be no deviation from the Post-Newtonian model.

Since in the past there has been no indication that the planetary motions might not be Newtonian, coordinates corresponding to a line element similar to (2.7) might still implicitly be used when processing the ranging data. Therefore, all estimated motions and parameters might be based on these coordinates. As an example consider the estimate of the distance between the Earth and the Moon. The LLR program estimates that the Moon drifts away by about 3.6 cm/year but the EST theory with the line element (2.1) predicts that the distance changes by about 1 cm/year. If the ephemerides were using the line element (2.7) with the coordinate r^’ we would have from (2.6) approximately r^’= r exp(t/T). Then dr^’/dt ~(dr/dt+r/T). The distance to the Moon is r=3.6 10¹⁰ cm. With dr/dtT=1 cm/year and T fourteen billion years we have dr^’/dt=3.6 cm/year.

3. Cosmological evidence for a curved spacetime.

If cosmological spacetime were curved it could mean that the cosmological redshift is a "gravitational" spacetime effect caused by spacetime curvature. With the line element (2.1) the redshift is "tired light":

I show in my paper (Masreliez, 1999) that this would solve several cosmological puzzles and explain the galaxy count and the angular size observations. It would also provide a simple explanation to the Pioneer 10 "acceleration" anomaly, which if there is tired light according to (3.1) would be given by:

The measured acceleration anomaly, a, is estimated at 7.5 10^-8 cm/s² (Anderson et. Al., 2002), which would imply T=13.3 billion years in excellent agreement with other estimates. Tired light also would explain the annual modulation of the observed anomaly.

4. Discussion.

Optical observations show that the planetary positions deviate from their ephemerides and strongly suggest that the planets accelerate. However, the ephemerides, based on radar ranging to the planets and laser ranging to the Moon, do not show evidence of any acceleration. This puzzling conflict might perhaps be explained if the cosmological line element is locally curved. In this case the presumption that the planetary motions are Post-Newtonian could lead to the use of a locally Minkowskian coordinate representation for which there are no planetary accelerations. With this choice of coordinates the ephemerides could be perfectly Post-Newtonian.

Thus, how observations are interpreted might depend on the coordinates used. Any investigation assessing the possible drift of the gravitational constant (or other deviation from the law of gravitation) based on traditional ephemeris fitting methods based on ranging measurements would implicitly use a local Minkowski-like line element and might not detect any such drift. In other words, if the ephemerides were constructed based on the assumption that the post-Newtonian model holds, range measurements alone would not disprove this law.

The individual ranging measurements are virtually identical for the two time-bases of (2.1) and (2.7). However, range discrepancies should, if they exist, become apparent over time. Since the uncertainties in the ranging measurements typically are of the same order as the predicted relative drift of the planets due to acceleration over a limited time interval of 20-30 years, deviations from the post-Newtonian model might not yet have been detected in the range measurements. However, it might be possible to resolve this question by comparing the dates and times of ranging measurements, recorded in atomic time, with the corresponding ephemeris dates and times derived from the ephemerides by inverse interpolation. In this way the existence of planetary acceleration could be tested using all available ranging data since the inception of planetary radar ranging.

On the other hand, modern optical observations do not depend on the Post-Newtonian model or on ephemeris time since they measure the planetary positions relative to the stellar reference frame recorded in atomic time. This might explain how they can detect secular acceleration of the planets in spite of their lower accuracy.

References:

J. Anderson et. Al., 2002, "Study of the anomalous acceleration of Pioneer 10 and 11", Phys.Rev. D65 (2002) 082004

Kolesnik Y. B., 1995, A&A 294, 876

Kolesnik Y. B., 1996, in Feeraz-Mello S., et. Al. (eds.) Dynamics, Ephemerides and Astrometry of the Solar System, Kluwer, Dordrecht, p. 477

Kolesnik Y. B., 2000, Applied Historical Astronomy, 24th meeting of the IAU, Joint Discussion 6, Manchester, England.

Kolesnik Y. B., 2001a, Journées 2000 "Systèmes de référence spatio-temporels", J2000, a fundamental epoch for origins of reference systems and astronomical models", Paris.

Krasinsky G. A., Pitjeva E.V., Sveshnikov M.L., Chunayeva L.I.,1993, Cel.
Mec. Dyn. Astron. 55, 1

Masreliez C. J., 1999, The Scale Expanding Cosmos Theory, Astroph. & Space Science, 266, Issue 3, p. 399-447

Oesterwinter C., Cohen C.J., 1972, Cel. Mech. 5, 317

Reasenberg R.D., Shapiro I.I., 1978, in "On the Measurement of Cosmological Variation Of the Gravitational Constant", L. Halpern, Ed., Gainesville, University Press of Florida, p.71

Seidelman P. K., Santoro E. J., Pulkkinen K. F. 1985, in Szebenhey V., Balazs B. (eds) Dynamical Astronomy, Austin, Texas, p. 55

Seidelman P. K., Santoro E. J., Pulkkinen K. F. 1986, in Kovalevsky J. and Brumberg V. A. (eds.) Relativity in Celestial Mechanics and Astrometry, Kluwer, Dordrecht, p. 99

Standish E. M., Williams J.G., 1990, in Lieske J.H. and Abalakin V.K. (Eds.) Inertial Coordinate System on the Sky, Kluwer, Dordrecht, p.173

J. G. Williams and E. M. Standish, 1989, "Dynamical reference frames in the planetary and Earth-Moon systems, in Reference Frames in Astronomy and Geophysics", editors J. Kovalevsky, I. I. Mueller, and B. Kolaczek, Kluwer Academic Publishers, pp. 67-90.

Standish E. M. 1998, "Time scales in JPL and CfA Ephemerides",
A&A, v. 336, p. 381-384

Williams, J. G., X X Newhall, and J. O. Dickey, "Relativity parameters determined from lunar laser ranging", Phys. Rev. D 53, 6730-6739, 1996.

Williams J. G., Anderson J. D., Boggs D. H., Lau E. L., Dickey J. O.,
"Solar System Tests for Changing Gravity", Amer. Astron. Soc., Pasadena, CA, June 3-7, 2001, Bulletin of the American Astronomical Society, Vol. 33, 836, 2001.

Williams, J. G., Boggs, D. H., Dickey, J. O., and Folkner, W. M., "Lunar
Laser Tests of Gravitational Physics", Proceedings of Ninth Marcel Grossmann Meeting, World Scientific Publ., ed. R. Jantzen, in press, 2001.

Yao Z-G., Smith C., 1988, in Débarbat S., Eddy J.A., Eichhorn H.K., Upgren A.R. (eds.) Mapping the Sky, Kluwer, Dordrecht, p.501

Yao Z-G., Smith C., 1993, in Muller I.I. And Kolaczek B. (eds.) "Developments in Astrometry and Their Impact on Astrophysics and Geodynamics", Kluwer, Dordrecht, p.403

Appendix

The geodesic equation of general relativity is:

From the variable transformation (2.6):

The geodesic equations for the radial and one of the angular coordinates are:

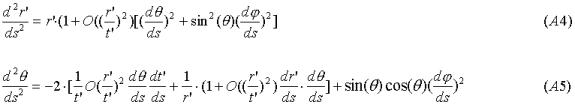
For ranging between the nearby planets at distances of about ten light minutes we have r^’/t^’= (10 minutes/14 billion years), which is about
10^-15.

From the coordinate transformation (2.6):

The relationship between the radial coordinates is: