THIS PAGE IS NOW BEING REVISED.
Gravitation in the Expanding Spacetime
1. Introduction
Schwarzschild's [Schwarzschild, 1916] solution to Einstein's field equations assumes that all components of the energy-momentum tensor for vacuum is equal to zero. However, the Expanding Spacetime (EST) theory [Scale Expanding Cosmos, Masreliez, 1999] proposed by the author implies an energy-momentum tensor for vacuum, the Cosmic Energy Tensor, with zero equivalent mass density but with non-zero components. I first show that a solution to Einstein’s equations similar to Schwarzschild’s external solution cannot exist with the Cosmic Energy Tensor of the EST theory. However, a minor modification to the Cosmic Energy Tensor permits a Schwarzschild type external solution. This modification implies that negative gravitational field energy must exist, which when integrated over space, is of the same magnitude as the gravitating mass energy. Thus, the gravitational field energy is reflected in the energy-momentum tensor. However, the solution does not permit the gravitational field to reach the event horizon since this would imply infinite spacetime curvature. This rules out Black Hole singularities. Instead of a Black Hole an object of maximum possible energy density might be formed. I propose a possible line element for such an object.
2. The Expanding Spacetime solution.
The line element for the Expanding Spacetime is [Masreliez, 1999]:

The angular measure is:
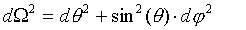
T is the Hubble time.
Following the usual approach we seek two functions of the radial distance, n(r) and l(r), that satisfy Einstein’s equations with an energy-momentum tensor for vacuum that equals the Cosmic Energy Tensor:

The constant, k, is Einstein’s constant. I will assume a central gravitating mass and a spherically symmetric line element of the form:
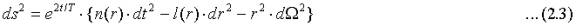
I showed in my earlier paper that this line element is invariant for translations in time due to scale invariance. It is therefore stationary. There also exists a cosmological reference frame. We are seeking the solution to Einstein’s general relativity equations:

In this relation Rij is the Ricci tensor and R the Ricci scalar.
Substituting 2.2 and 2.3 into Einstein’s equations (2.4) we get the following equations after setting exp(L) = l(r) and exp(N)= n(r):


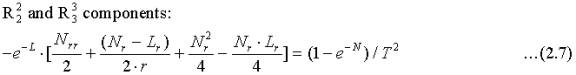
The subscript r stands for differentiation with respect to r. These equations have the trivial solution N = L = 0 when the line element coincides with the line element for the Expanding Spacetime.
There is no solution corresponding to Schwarzschild’s solution. Substituting (2.5) and (2.6) into (2.7) we get:
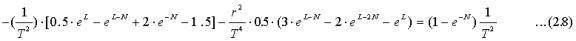
Since exp(L) becomes very large and exp(N) small near the horizon a Schwarzschild type solution does not exist unless the mass accumulation modifies the vacuum energy-momentum tensor.
Let us assume that Nature has chosen the two functions l(r) and n(r) such that both relation (2.5) and (2.6) are satisfied exactly. To the first order in (1/r) in the far field the solution takes the form:


The function F may for r>>r0 be approximated by:

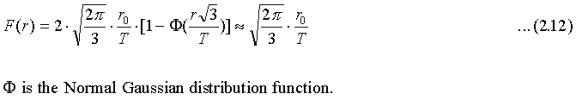
The two functions (2.9) and (2.10) satisfy relation (2.8) to the first order in (r0/r) except for a rest term formed by subtracting the right hand side of (2.8) from the left hand side:
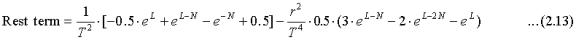
If this rest term is added to the right hand side, relation (2.8) holds in the far and intermediate range for which r >> r0. In the far field we have:
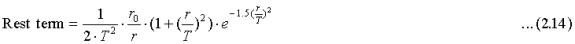
Far away from the gravitating object the influence of the gravitational field is truncated at a distance comparable to the Hubble distance. This is a desirable feature in a universe of possibly unlimited extension since the gravitational potential always is bounded. One of the bothersome aspects with the traditional gravitational potential is infinite in a flat universe with constant mass density:

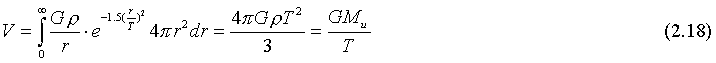
Mu is the total mass within a sphere in the universe with radius T. This pleasing result tells us that the gravitational potential everywhere in the EST universe is bounded and equals the classical potential on the surface of a sphere of radius T.
Very close to the horizon at r = r0 the function S dominates and, as we shall see, prevents gravitational collapse. It is interesting that both the far field and the near field properties of the gravitational field are significantly modified by the energy-momentum tensor induced by the scale expansion, while leaving the intermediate field essentially the same as the Schwarzschild field.
Since it appears that a Schwarzschild type solution actually exists in Nature it suggests that the presence of mass might modify the vacuum energy-momentum tensor by the small negative energy density corresponding to the terms (2.13) and (2.14). I will show that this energy density when integrated over the whole space corresponds to a negative energy of the same order as the gravitating mass.
The scale expansion will also generate a radial momentum flux:

This outwardly directed momentum flux increases sharply close to the e`vent horizon.
3. The gravitational field energy
The energy seen by an observer depends on the observer’s frame of reference. In a universe with no preferred reference frame like in the standard Big Bang model, the vacuum energy is always zero regardless of the reference frame.
However, the situation is different in the EST since the scale expansion defines a reference frame. This makes it natural to measure the cosmic energy relative to this reference frame. We do this when assigning a certain energy density to vacuum - the Cosmic Energy Tensor in the EST. The scale expansion defines a reference frame and also the cosmological energy-momentum tensor relative to this frame.
In a stationary situation like the EST universe, the energy within a spatial region may be assessed by the volume integral:

I have ignored the exponential scale factor in (2.2) due to scale invariance that permits us to set t = 0 at any epoch. The volume element dV* is the invariant (√–g )dV where g is the determinant of the metric tensor, dV is the spatial volume element and the integral is evaluated in the cosmic reference frame. Assuming spherical symmetry we get:
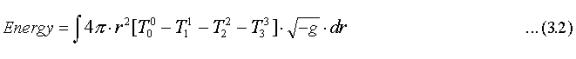
The energy-momentum tensor given by (2.2) does not contribute to this integral but the rest term (2.14) does. Integrating the contribution from (2.14) from some radial distance ri with r0<< ri <<T we get since (√–g ) ≈1 in this region:
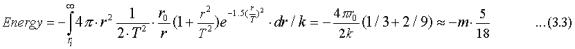
Above I used two familiar relations with c = 1:

Thus, the two angular relations (2.7) together contribute -5mc2/9 = -0.56mc2 to the gravitational field energy.
This suggests that the creation of matter, i.e. of positive energy, may be accompanied by a negative energy contained in the gravitational field in the form of a modification to the vacuum energy-momentum tensor. Since l(r) goes to infinity and n(r) to zero at the event horizon, the negative energy density approaches infinity at the horizon according to (2.13). Therefore, the gravitational field cannot be extended all the way to the horizon.
This suggests that there can be no Black Holes in Expanding Spacetime.
4. The scale expansion prevents Black Hole formation
The solution (2.16) implies that there is a true gravitational singularity at some Critical Radius (CR) r = rc close to the Schwartzschild event horizon r0. The Riemann curvature tensor is given by:
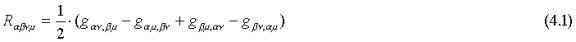
Consider the two first terms and third terms and let the two first indices in the first term and two last indices in the third term be zero. Also, let the two last indeces and the two first indices in respective terms be one. The third term g11,00=4g11/T2 becomes infinite at rc and the first term g00,11 is finite. Therefore, the corresponding element in the Riemann tensor is infinite; spacetime curvature is infinite at the critical radius and we have a true spherical singularity at r = rc instead of a point singularity at the origin as in the standard model. Next I will show that a freely falling particle never reaches the CR.
Consider a test particle falling radially in the gravitational field generated by the line element given by (2.3). The geodesic for this motion is given by:

This becomes with the metrics of the line element (2.3)::
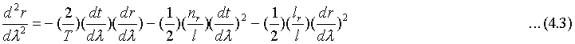
The first term is the for the EST universe unique "cosmic drag". It represents acceleration in the opposite direction to the motion of the test particle. Obviously this acceleration will tend to slow down the fall of the particle and will to some degree help prevent gravitational collapse. The last two terms are of the same form as for a particle falling under the influence of gravitation generated by the line element (2.3) without the exponential scale factor. It is therefore sufficient to consider relation (4.3) without the first term but with metrics n(r) and l(r) as in (2.16). Since these metrics are independent of time the temporal component of the four-momentum vector is a constant of motion.

The four-momentum also satisfies:

Substituting (4.4):

Dividing through by m2 and recognizing that parameter lambda equals the proper time, tp for the falling particle we get:

In the standard model the Schwarzschild metrics are given by:


Since this proper velocity always is finite we have the well-known result that the test particle with the Schwarzschild metric may continue falling right through the event horizon. It is swallowed by a Black Hole.
This is not true in the EST universe. Adding the two relations of (A1) in the Appendix and integrating we have:

Substituting this relation into (4.7) and making use of (2.15) we find that the velocity close to the event horizon r = r0 satisfies:

The gravitational field can therefore never pull matter inside the event horizon. This is consistent with the observation I made above that the gravitational field can not be extended all the way in to the event horizon.
This suggests that Black Holes do not exist in the EST universe. There are no point-like singularities; all particles must have finite extensions.
5. An Object of Maximum Energy Density
If matter never can reach the event horizon and a Black Hole cannot form what happens at a gravitational collapse? The only possibility is that the contraction stops just short of collapse into a Black Hole, forming an object within which all matter lies immediately outside the (relative) event horizon. Within this maximum mass density object a mass particle at a distance r from the center lies just outside the event horizon corresponding to the matter inside the radius r. This implies that the gravitational field inside the object must be zero since there can be no acceleration in the radial direction at any point. This implies n(r) = constant. I will therefore assume that negative field energy density E exists corresponding to a positive term on the right hand side of equation (2.6) that exactly balances the gravitational field generated by the mass inside the object so that:
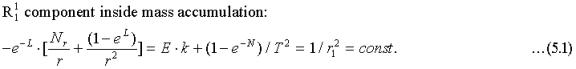
where

The solution is:

This solution also satisfies the remaining equations:
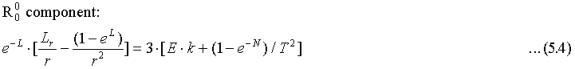
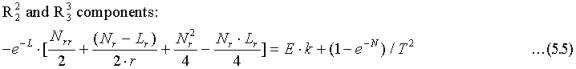
Identifying the right hand terms with the components of an energy-momentum tensor, we find that like the Cosmic Energy Tensor of the EST theory this is a tensor with zero net gravitational energy, since the sum of the three spatial components equal the temporal component. Therefore the gravitating field energy is zero inside the maximum energy density object as expected.
The undetermined constant values for the temporal metric, ni, and the distance, r1, are to be determined by boundary conditions.
Obviously, this interior solution does not apply to the exterior where the Schwarzschild type solution (2.9) and (2.10) applies. However, the new solution could apply in the region r < rp.
It is possible to piece together continuous metrics for both space and time by combining the two solutions. This will work if we chose the radial distance, rp, at the interface between the solutions as follows (l(r) and n(r) are the solutions of (2.5) and (2.6)):

It is always possible to do this since ni(r) is a freely selected constant. In the standard model with zero energy-momentum tensor (5.1) implies:

6. The gravitating energy of the new solution.
From the chosen form of the energy-momentum tensor we already know that the energy contribution from the volume inside the radius rp is zero. However, both Nr and Lr have discontinuities at r = rp where the two solutions are patched together.
Integrating (2.5) and (2.6) over an infinitesimal interval surrounding rp we find that the contributions from T00 and T11 are zero since both Nr and Lr are bounded. However, the two angular components T22 and T33 given by (2.7) provide an energy contribution given by:
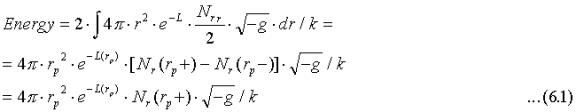
Thus, the energy is located in a shell of radius rp and is given by:

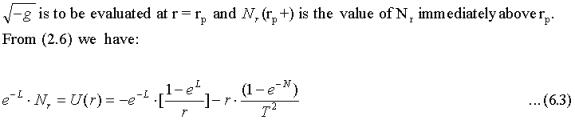
The equivalent energy density in the region inside the shell is zero.
In the standard model with the Schwartzschild solution the energy in the shell becomes:

The volume inside the shell contains canceling positive and negative energy densities 3·[E·k -exp(-N)/D2]/k = (3/r12)/k. If the positive energy density arises from the mass compacted inside the object we note that integrating this density over the region r < rp in the standard model we find that the mass energy inside the shell is:

Thus, in the standard model the energy of the shell equals the energy of the mass that generates the gravitational field. However, note the curious fact that in this case the distance rp is completely arbitrary. The energy of the shell is independent of its radius.
However, in the EST universe the distance rp may be determined by postulating that the positive energy of the gravitating shell equals the negative energy of the gravitational field. This reasonable postulate is based on the assumption that matter energy and gravitational energy cancel in the Universe.
7. Discussion.
Schwarzschild's external solution crucially depends on the assumption that the vacuum energy density is zero. If this is not the case Schwarzschild's solution no longer applies. This might eliminate Black Hole type singularities. I derive a spherically symmetric solution to Einstein's General Relativity relations assuming that the energy-momentum tensor for vacuum is as proposed by the [Masreliez, 1999]. Although the equivalent mass density vanishes everywhere this vacuum energy-momentum tensor contains non-zero components. With this Cosmic Energy Tensor the possibility of Black Hole formation disappears.
Some of the results of this article are based on the crucial assumption that the solution to Einstein's equations with the Cosmic Energy Tensor of the EST theory satisfies the two relations (2.5) and (2.6), which implies that they at the same time cannot satisfy (2.7). It is quite possible that Nature may have selected another approach and that all three GR relations are violated to some extent. However, the solution chosen by Nature, whatever it might be, should not remove the singularity at the critical radius, which prevents Black Hole formation.
In the standard model the Schwarzschild's solution implies that a freely falling test particle in a gravitational field could be pulled into a Black Hole. However, a Schwarzschild type solution to Einstein's field equations does not exist in the Expanding Spacetime unless spacetime contains negative energy density in space surrounding the gravitating mass. However, this field cannot be extended all the way into the horizon since this would imply infinite field curvature.
Thus, there can be no Black Holes in the Expanding Spacetime. This is comforting since a universe without Black Holes ought to be considered more plausible than a universe permitting them. The fact that the standard assumption that the energy-momentum tensor is zero permits Black Holes strongly suggests that the energy-momentum tensor for vacuum may not be equal to zero. Much time and effort has been expended trying to make sense of the Schwarzschild solution inside the event horizon. Perhaps this solution simply does not apply since the region inside the event horizon is forbidden.
It is widely accepted that the gravitational field surrounding a mass element contains negative energy that seems to balance the positive mass energy. However, in the standard model with zero vacuum energy density there is no trace of gravitational field energy in the energy-momentum tensor. This is puzzling since the negative energy of the gravitational field ought to express itself in the energy-momentum tensor relative to some reference frame. Yet, all components of this tensor are zero regardless of frame of reference. On the other hand, in the EST where a definite cosmological reference frame exists one finds that a gravitational field cannot exist without modifying the vacuum energy momentum tensor and create negative field energy relative to this reference frame.
In the EST a particle falling in a gravitational field never reaches the event horizon. This suggests that matter may accumulate at a maximum possible density within which all particles barely lie outside "their relative" event horizon created by matter closer to the center of the mass accumulation. I present a solution to Einstein's GR equations that models such a saturated mass accumulation. The metrics for this solution could continuously interface with the exterior solution close to the event horizon.
The line element for the interior of this saturated mass density object is approximately:
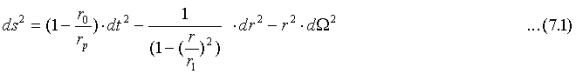
This line element corresponds to a closed three-dimensional space with radius r1>r0. It is interesting to note that Einstein originally proposed this type of closed space (Einstein, 1917) as a model for the universe. However, since the radius rp of the gravitating object lies just inside r1, the interior region is not completely closed.
One could perhaps speculate that saturated energy density objects naturally are formed in the center of galaxies where they could prevent the formation of Black Holes. They might be the engines of quasars. The activity involved in preventing gravitational collapse could be the source of their intense radiation.
References.
Einstein A., "The Foundation of General Relativity Theory", Ann. Physik 49:769-822 (1916)
Masreliez C.J., The Scale Expanding Cosmos Theory, Astroph. & Space Science, 266, Issue 3, p. 399-447 (1999)
Schwarzschild K., "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie", Sitzber. Deut. Akad. Wiss. Berlin, Königl. Math. - Phys. Tech. 189-96 (1916)
Appendix
Very close to the event horizon:

The velocity of a falling particle is at the event horizon:

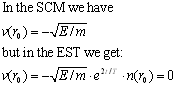
Particles falling on geodesics will not cross the event horizon. Thus the EST scale expansion could both limit the range of the gravitational potential far away by the factor exp[-1.5(r/T)2]and prevent the formation of black holes. The spherical event horizon at r=r0 is a true singularity in the EST.
Although interesting, these observations are not conclusive since there is no exact solution to the GR equations. The only thing we can say with certainty is that any spherically symmetric solution necessarily must modify the energy-momentum tensor.