EST

Expanding Spacetime Theory

EST Home

On the shape of spiral galaxies and their flat rotation curves.

C. Johan Masreliez

1. Introduction.

In an earlier paper (Masreliez, 1999) the author proposed that the universe might evolve by changing the metrics of both space and time. This mode of expansion might resolve several cosmological puzzles. An interesting aspect of the new model is that it implies a new phenomenon, cosmic (velocity) drag, which diminishes the relative velocities of freely moving particles as well as the angular momentum of freely rotating systems. In this paper I show that cosmic drag not only would explain the spiral shape of galaxies but also their flat velocity curves.

The new theory, which here is referred to as "The Expanding Spacetime (EST) theory", is based on the observation that the equations of general relativity are the same for line elements with different metric scales, which suggests that the spacetime geometry of the universe could remain unchanged during a cosmological scale expansion of both space and time. In such a scale expansion of all four metrics there would be no reference epoch; all epochs would be equivalent. However, when modeling such an expansion mode in general relativity one finds that there is no continuous variable transformation connecting different epochs. With a continuously expanding scale different epochs are not covariant and are therefore not physically equivalent in the Einstein sense. Some researchers have extended the scope of general relativity to include a changing scale, for example Weyl's modification to general relativity, which also was considered by Dirac and more recently by Canuto and by Maeder in a series of articles. The EST theory takes a different approach by assuming that the cosmological expansion occurs in discrete temporal increments

2. Summarizing the EST theory.

Since this new theory is not yet very familiar, a brief summary is warranted. The philosophical line of reasoning that leads to the EST theory starts with the proposition that the cosmological scale of material object and dynamic processes is relative and that no absolute scale of things exists in the universe. Not only does this relativity of scale make intuitive sense, since it is difficult to understand why any particular scale should take preference in the universe, but it also agrees with known physics, which recognizes scale invariance as a well-known example of gauge invariance.

Therefore, I make universal scale invariance a first postulate:

P1: There is no absolute scale of the spacetime metrics.

However, in general relativity this gauge invariance might seem quite trivial since a different scale may be though of as simply a re-definition of the metrics of spacetime so that different scales merely correspond to different units of measurement. Although this is true if the scale remains constant, the cosmological expansion raises the question whether the cosmological scale might change with time. A with time expanding scale would create a universe with different properties compared to a universe with fixed scale. Since general relativity does not distinguish between different scales and since there seem to be no reason why any particular scale should take preference it appears reasonable to assume that if the universe expands by changing the scale both of space and time, different epochs are geometrically and physically equivalent. This reasoning leads to the second postulate:

P2: All spatial and temporal locations are physically equivalent in all respects.

If the scale of both space and time increase with the progression of time we could attempt to model this in general relativity by a time dependent scale factor, a(t), multiplying all four metrics in the line element. This would model a universe where spacetime expands relative to a fictitious coordinate system with fixed rate of (proper) time as given by the invariant ds. Based on the two postulates above we conclude that the cosmological scale expansion must be exponential with time. In this case the line element with scale factor exp(t) is equivalent to the line element with scale factor exp(t+Δt) = constant·exp(t), since spacetimes differing by a constant scale factor are equivalent according to general relativity. This suggests that different epochs are physically equivalent. However, according to general relativity this equivalence can only be obtained between spacetimes of differing scales corresponding to some time increment Δt. Then these two line elements are related via the simple transformation t2= t1+ Δt and therefore strongly equivalent in the sense of Einstein. However, no continuous variable transformation exists connecting different line elements with scale factors exp( t1) and exp(t2). This suggests that the requirement that all epochs are equivalent (covariant) in the sense of Einstein implies that the cosmological expansion occurs in discrete temporal increments. We thus arrive at a third postulate:

P3: The cosmological expansion takes place in discrete temporal increments.

Together these three postulates form the basis for the Expanding Spacetime theory. The third postulate also follows from the impossibility of conceiving a pace of time that changes continuously relative to it self. The EST theory bypasses this problem by introducing the scale as "a fifth dimension" beyond the four dimensions of spacetime.

If we model the cosmological scale expansion by a line element with an exponentially increasing scale factor relative to a fictitious non-expanding coordinate system, how should this be modeled in a coordinate system that expands together with spacetime? To an observer in this expanding spacetime the relation between the metrics of space and time would always remain the same, but there would be additional physical effects due the exponentially accelerating scale. At every instant t= Δt the universe would "look the same" as it did at t=0. One possible way of modeling this mode of expansion is the following iteration loop:

General relativity is "blind" to the change of proper time in the second step since the line element remains the same at t and t+ Δt and the energy-momentum tensor does not change.

However, the new and different aspect of this cosmological expansion mode is the discrete change of the pace of time in the second step. This takes the EST model beyond general relativity and established epistemology, which presumes continuous processes. One may well wonder if this radical departure is justified.

In response to this question, consider the nature of "motion". How does a moving particle change its position with time? This was an unresolved mystery for the antique Greeks, but since the seventeenth century, with the introduction of differential calculus, we treat motion as a limiting process of infinitely many incremental, diminutive, steps. Since this works excellently when modeling macroscopic motion, we usually handle the dynamics of moving objects by solving differential equations assuming continuous progression of time.

Although we take the validity of continuous motion for granted, upon deeper reflection this idea seems rather strange. In fact, it is difficult if not impossible to think of motion as a continuous process. We are always visualizing motion as a sequence of small incremental displacements. The difficulty with continuous motion is that it seems to imply that an infinite number of steps must occur in a limited time. The ancient Greeks recognized this puzzle as one of Zeno's paradoxes. More recently, quantum mechanics has revealed that the nature of the quantum world is discrete rather than continuous.

The very natural idea of implementing motion by a sequence of consecutive steps might actually be Nature's way. Continuous motion might never occur in Nature. The progression of time might very well be discrete, and the modeling of particle trajectories by differential equations might fail in the quantum world.

In addition to this somewhat philosophical argument I offer the following comments:

The EST model, which implies discrete progression of time, better agrees with astronomical observations than the Standard Model based on the Big Bang and it resolves several cosmological puzzles. It also predicts a new phenomenon, cosmic drag, which not only explains the spiral form of galaxies but which also already might have been detected by observations in the solar system (Kolesnik, 2000, 2001).

Second, nothing is wrong with the idea that the scale of the universe might change with time and that all epochs are equivalent. Everyone easily grasps this cosmological expansion mode. However, such a continuous scale expansion process cannot be modeled by general relativity and therefore has not been seriously considered in the past. But, we ought to be able to model a cosmological scale that expands with time. The fact that we cannot do this indicates a weakness in available mathematical models rather than a constraint to be imposed on the way the universe works. In short, the fact that we cannot model it by general relativity does not mean that it cannot be.

3. A few properties of the Expanding Spacetime model.

The Expanding Spacetime theory has proven remarkable capable of solving several cosmological puzzles and its predictions excellently agree with observations (Masreliez, 1999). Some of the advantages of the EST model are summarized below:

This paper discusses the effect cosmic drag would have on the motions of stars in a galaxy.

4. Cosmic drag - a new cosmological phenomenon.

The Expanding Spacetime theory line element is given by:

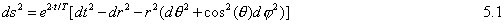
T is the Hubble time commonly associated with the age of the universe. In deriving the corresponding geodesic (see Masreliez, 1999) we find that a particle initially moving at the speed of light always will move at the speed of light. However, relative velocities of freely moving slower particles will diminish with time. If the velocity is much less than the speed of light we have:

Similarly, rotating systems will lose angular momentum. For slow rotations we have:

A freely moving particle with initial velocity β=v/c will slow down and eventually stop at a distance L (this expression is wrong in my previous paper):

The relativistic Doppler shift is given by:

and we have:

Thus, the Doppler shift corresponding to the initial velocity is the same as the cosmological redshift at the ultimate range, L, where the particle has come to rest. The redshift actually is constant (see the Appendix) for a freely receding or approaching particle in the EST universe regardless of the distance. In the Standard Cosmological Model, the particle moves at constant velocity all the time, but in the EST universe it coasts to a stop due to cosmic drag at a distance where the cosmological redshift equals the initial Doppler shift.

Relation (5.3) may be combined with Kepler's third law for planetary motion,

to derive the two relations:

Figure 1

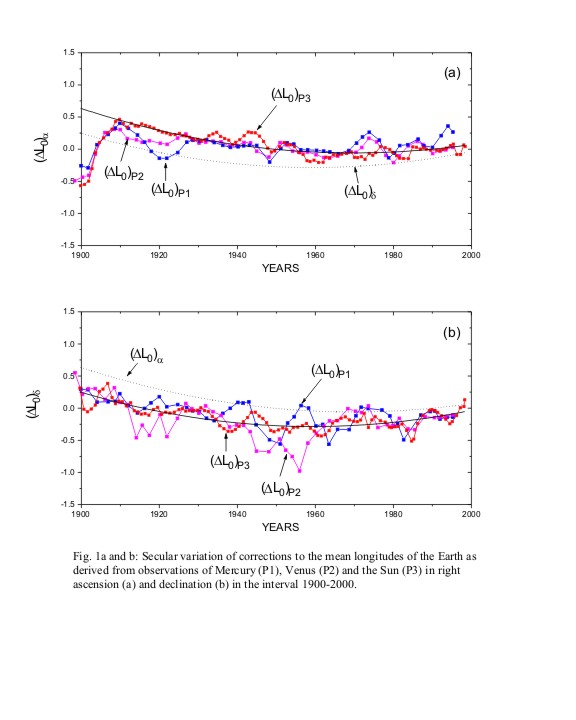
Figure 2

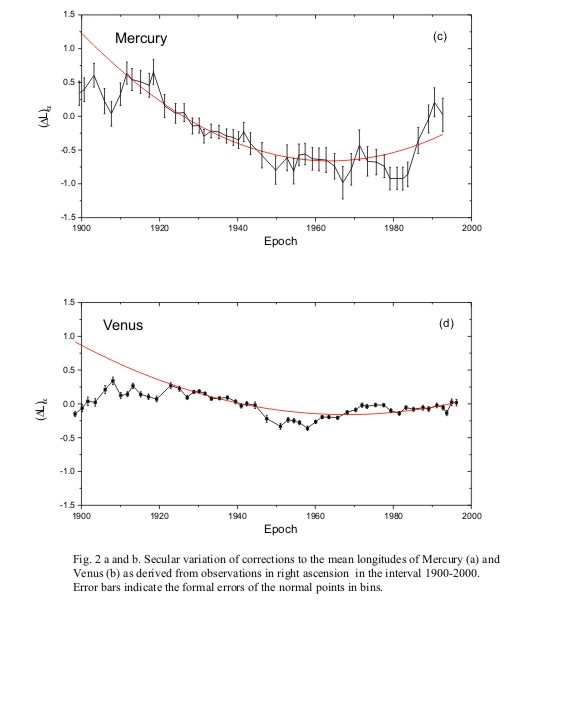
The last relation explains the angular acceleration of the planets in the solar system. Figures 1 and 2, which are from Kolesnik's paper (Kolesnik, 2000), show the observed angular accelerations of the inner planets. These measured accelerations agree with (5.9) if the Hubble time is about 14 billion years. For the Earth the EST acceleration is about 2.7 arcsec/century squared (2.7"/cy2) and the Earth approaches the Sun by about 25 meters/year.

Combining the geodesic with the gravitational potential we get the following expression for the radial acceleration (see Masreliez, 1999):

The first term is very small, and I will assume that the expression within the brackets on the average disappears:

We see that for a concentrated central mass, M(r)=constant, the radial distance decreases with time as in (5.8). However, other mass distributions might give different decay rates.

The average (tangential) velocity at some radial distance r is as usual:

5. Stellar motions in galaxies.

With these preliminaries we are in position to investigate the motion of stars in galaxies. Expression (5.11) provides information on radial decay rates as a function of the radial distance and time. For example, if the mass of the galaxy increases linearly with the radius we see that a radial decay rate proportional to exp(-t/T) will satisfy (5.11). Using the velocity relation (5.12) we then find that the velocity is constant so that the velocity curve is flat, which agrees with observations in spiral galaxies.

Cosmic drag causes the stars in a galaxy to fall slowly in spiral trajectories toward the galaxy core. Since the stars and other matter fall along geodesics there is no shear effect and gravitational attraction can work unimpeded to gather matter into two or more arms that form a thin rotating disc. However, this is not possible by standard physics. Simulations show that the arms will not form and matter will not collect in a thin disc due to the shear effect caused by the radial velocity gradient and dynamic instabilities. In the EST model dynamic instabilities are damped out by cosmic drag.

Relation (5.11) shows how the radial distance decays for different mass distributions M(r) as a function of the radius. Assume that the radial distance of a star decays according to:

Let's first assume that A is constant. Considering a small time increment, t, we get from (5.11):

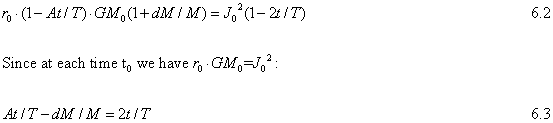
We already saw that with M(r)=const · r we get A =1. With M(r)=const · r2 corresponding to a homogenous disc, we get from (6.1) dM/M=-2A and then from (6.3) A= 2/3 and with M=const · r3 corresponding to a homogenous sphere we get A=1/2.

If the mass flow in a typical spiral galaxy is in a steady state, the amount of matter falling inward is constant independent of the radial distance; otherwise the mass density would either increase or decrease with time in some regions. Thus we have for a spiral galaxy in steady state:

Using (6.4) we get:

The total mass in the region between two radial distances is proportional to the time it takes for a particle to fall through the region. Note that the thickness of the disc does not influence this result.

Let's consider a few different possibilities:

Case 1: The radial velocity vr is independent of the distance. In this case M(r)=Mc+ const · r and we saw that the velocity curves are nearly flat for large distances r.

Figure 3

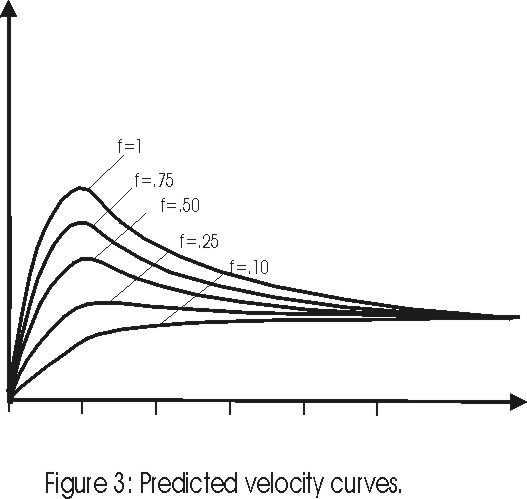
Figure 3 shows the resulting velocity curves for a few different central mass accumulations. In this figure f is the fraction of the galaxy mass inside the radius 5rc , M(5rc), that is confined within r<rc, where rc is the diameter of the central bulge, i. e. Mc =f · M(5rc).

From the angular momentum relation (5.3) and from (6.1) and we get:

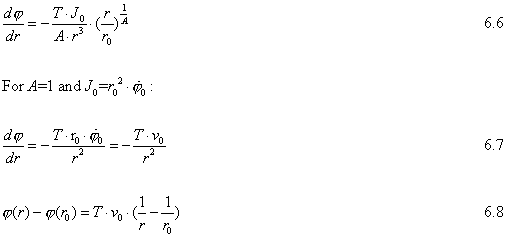
The shape of a galaxy arm is formed by the trajectory of a star relative to the rotation of the galaxy at r=r0 where the angular velocity is v0/r0. With A=1 this relative angular displacement is:

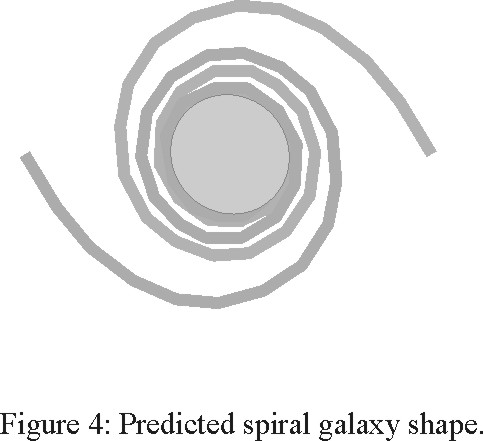
This shape is shown in Figure 4. As an example consider r = 30,000 light years and v=200km/s then with T=14 billion light years we find from (6.8) that the radial distance decays by about 650 light-years per revolution, which takes about 270 million years.

Figure 4

Case 2: From (5.11) the radial in-fall velocity increases with increasing distance. If (6.1) applies, the radial velocity is proportional to the distance and the mass density is:

The mass function now is:

The corresponding velocity curves shown in Figure 5 are very similar to those of Figure 3, the only difference being a slight fall-off with increasing radius.

Case 3: For completeness, consider Case 2 with the added assumption that the time "constant" A changes with the radius. We might for example consider:

By this assumption the time constant A(r) increases from A(rc)=1/2 corresponding to a spherical mass distribution to A(r)=1 at large distances.

Figure 5

The mass function then becomes by (6.10):

The corresponding velocity curves are almost identical those of Figure 5 showing that flat velocity curves is a generic feature of spiral galaxies in the EST universe.

Discussion

According to the Expanding Spacetime theory velocity drag of cosmological origin influences the motion of all freely moving and rotating bodies. This new phenomenon explains the spiral shape and stability of galaxies and their flat velocity curves. Cosmic drag also predicts that the planets in our solar system slowly spiral toward the Sun with accelerating angular velocities. This phenomenon has recently been detected from worldwide optical observations during the last fifty years with atomic time. Cosmic drag will cause stars that freely fall on geodesics to flow toward the galaxy core. This eliminates the destabilizing effect of shear forces between radial layers moving at different velocities, which is characteristic of standard physics. Cosmic drag also dampens out dynamic instabilities. It is shown that flat velocity curves directly could result from the steady state streaming of matter toward the galaxy core and that these velocity curves are fairly insensitive to the actual composition of the galaxy disc. This explanation eliminates the need to postulate the existence of galactic dark matter halos.

Appendix

The geodesic of a freely moving particle in the EST universe is (Masreliez, 1999):

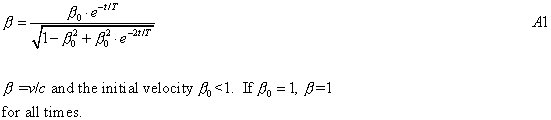
The distance traveled by the particle at time t is:

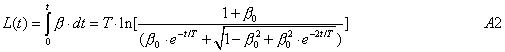
The EST tired light redshift relation is:

From (A2) the cosmological redshift the distance L(t) is given by:

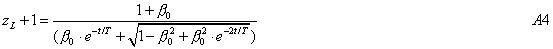
On the other hand, the Doppler shift is given by:

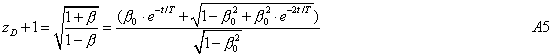
The total redshift is the product of these two factors:

In the EST universe the cosmological redshift of a source, which recedes or approaches on a geodesic, is constant regardless of the distance giving the false impression that the source always moves at the same velocity.

References

Canuto V., Adams, P.J., Hsieh, S.H. and Tsiang F., 1977: Phys. Rev. D, 16, 1643

Dirac, P.A.M, 1973: Proc. Roy. Soc. London A 333,403

Kolesnik Y. B. 2000: Proc. IAU, 2000

Maeder, A., 1977: Astron. Astrophys. 65, 337-343

Masreliez C. J. 1999: Astroph. & Space Science, 266, Issue 3, p. 399-447

Back to Top