Analysis of the secular variations of longitudes of the Sun, Mercury, and Venus from optical observations.
Y.B Kolesnik
Institute of Astronomy of the Russian Academy of Sciences, Piatnitskaya str. 48, 109017 Moscow, Russia
1. Motivation
Comparisons of optical observations reduced to the FK5 system with DE200 show significant linear trends of residuals, see Yao & Smith (1988, 1993), Standish & Williams (1990), Seidelman et al. (1985, 1986), Kolesnik (1995, 1996). The present study was primarily motivated by a desire to interpret the large discrepancy between numerical ephemerides and the 20th century optical observations. Other objectives were: a) to check the level of consistency between early observations of the 18th and 19th centuries and numerical ephemerides; b) to assess of the actual scientific content of the early observations in view of the recent accuracy achieved by astrometry; c) to revise of the value of the tidal acceleration of the Moon; d) to estimate the ICRS offset with respect to dynamical equinox and its possible residual rotation.
2. Observations
A mass of 244,960 observations of the Sun, Mercury and Venus accumulated during the historical period of astronomy were incorporated. All the observed material can naturally be divided into three periods: 1750-1830, 1830-1900 and 1900-2000. The first one can be characterized as a period of formation of classical astrometry. Observations in this period were re-reduced later by Bessel, Airy, Le Verrier, Auwers and Knox-Show. In the second period the quality of instruments and methods of investigation progressively improved and observations of the daytime objects reached nearly 1 arcs econd ( arcs ) accuracy. At the beginning of the 20th century the moving-wire micrometer was introduced into common practice significantly reducing personal errors. Typical internal errors of instrumental series in the 18th century observations of the daytime objects is 2 arcs in right ascension and 1.5 arcs in declination. The best instruments of the second half of the century reached some 0.5 arcs -0.8 arcs . The level of 0.5 arcs has remained typical for the 20th century observations.
3. Transformation of observations onto the ICRS frame and method of analysis
In the transformation procedure a set of corrections were formed by direct comparison of a standard star catalogue with the ICRS-based catalogue rotated from J2000 to the respective epoch by use of modern precession constant and Hipparcos based proper motions. The systematic differences are interpolated onto the observed positions of planets. Other corrections account for differences in modern and historical astronomical constants. The N70E catalogue (Kolesnik 1997) rigidly rotated onto Hipparcos frame was used as a reference catalogue. Observations were compared with DE405 ephemeris. The series (ET-UT) by Stephenson & Morrison (1984) were applied before 1955. After 1955 ET is equal to TDT or TT and directly related to atomic time TAI.
Conditional equations for the Sun are the same as applied by Newcomb. For Mercury and Venus these are the same as given in Kolesnik (1995). The secular variation of the corrections to the longitudes was determined separately from right ascension and declination residuals. In the conditional equations for right ascensions the equinox correction is omitted assuming that it will be absorbed in the solution by corrections to the longitude of the Earth. Corrections to the longitudes were derived in relatively short time span bins, and evaluation of secular variations of longitudes was based on a set of stepwise individual solutions in bins. Corrections to the mean longitude of the Earth ΔL0 were determined from the right ascension and declination residuals of all objects. Corrections to the mean longitudes of Mercury and Venus ΔL resulted from residuals in right ascension only.
Figure 1a
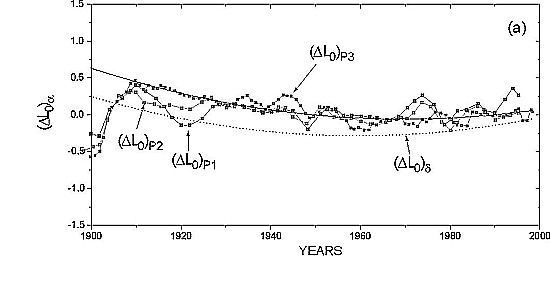
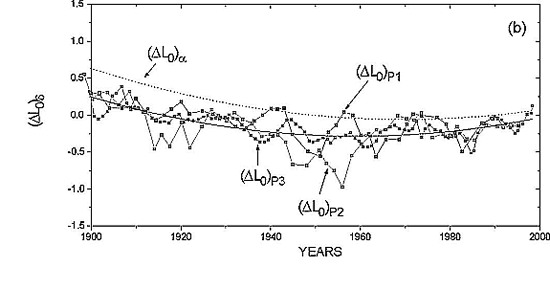
Figure 1b
4. Results
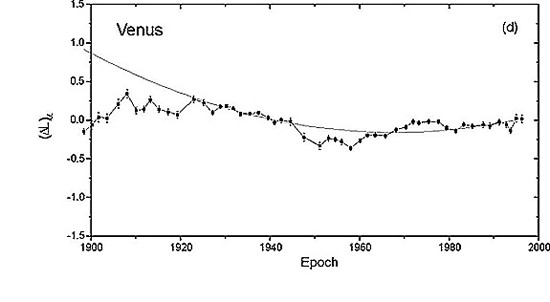
The individual solutions tracing the secular variations of the longitudes of the Earth ΔL0 resulting from right ascensions and declinations of the Sun, Mercury and Venus during the 20th century are presented in Fig. 1a and b. The corresponding corrections to longitudes of Mercury and Venus ΔL are presented in Figure 2a and b. L0 solutions derived from observations of different objects are highly consistent. In the 20th century longitude corrections derived from the Sun and both planets have quadratic trends nearly proportional to the respective mean motions. Their second order approximations are presented in Table 1.
Table 1. Second order approximations of the trends in secular variations of the longitudes of the Earth ΔL0 and Mercury and Venus ΔL in the 20th century. Index indicates from which kind of observations (right ascensions or declinations) longitude corrections are derived. T = (t-1960)/100 with t in years. All entries in arcseconds. T0 is the constant term, T1 the linear and T2 the quadratic coefficient.
| T0 | T1 | T2 | |
|---|---|---|---|
| Sun (ΔL0)α | -0.05▒0.01 | -0.28▒0.01 | 1.42▒0.04 |
| Sun (ΔL0)δ | -0.28▒0.01 | +0.02▒0.02 | 1.51▒0.10 |
| Mercury (ΔL)α | -0.80▒0.03 | -0.89▒0.10 | 4.51▒0.41 |
| Venus (ΔL)α | -0.20▒0.01 | -0.30▒0.03 | 2.78▒0.15 |
Since
ΔE=(ΔL0 )δ-(ΔL0 )α
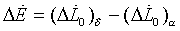
at the epoch J2000.0: -0.10 ▒0.01 arcs and d(ΔE)/dT= + 0.30 ▒0.03 arcs /cy
Figure 2a
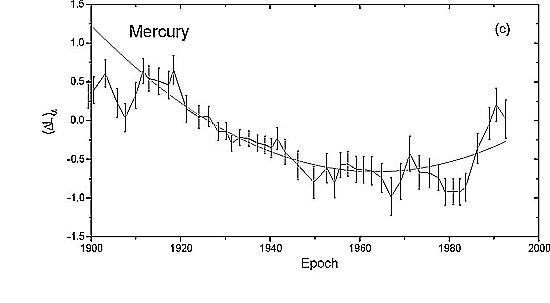
Figure 2b
5) Interpretation of the secular trends in longitude corrections
The dependence of the trends on mean motions provides evidence that some acceleration factor affects the comparison results. The Expanding Spacetime (EST) theory (formerly Scale Expanding Cosmos theory) by Masreliez (2000) predicts accelerations of the planets in the Solar system according to the relation dn/dt=3n/T Hubble time). For Mercury, Venus and the Earth the predicted secular accelerations are 5.7, 2.3, and 1.4 arcs/cy2, i.e. of the same order as the actually detected quadratic terms presented in Table 1 if the T is fourteen billion years. This value for the Hubble time agrees with the most recent estimates from other sources.
Fig. 1a and b. Secular variation of corrections to the mean longitudes of the Earth as derived from observations of Mercury (P1), Venus (P2) and the Sun (P3) in right ascension (a) and declination (b) in the interval 1900-2000.
Fig. 2 a and b. Secular variation of corrections to the mean longitudes of Mercury (a) and Venus (b) as derived from observations in right ascension in the interval 1900-2000. Error bars indicate the formal errors of the normal points in bins.
6) Interpretation of the equinox drift
Residual rotation of proper motion systems of the principal compiled catalogues of the 19th and 20th centuries was investigated by their direct comparison with Hipparcos motions. The results are given in Table 2.
Table 2. Estimation of the residual rotation Δε and correction to adopted precession constant (Δp1) of historical compiled catalogues from their direct comparison with Hipparcos proper motions in the equatorial zone. All estimates are in arcs ec/cy.
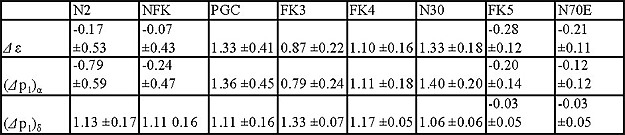
Direct comparison with Hipparcos of the catalogues constructed before the FK5 indicate (Δp1)δ correction to Newcomb's precession close to Fricke╣s correction 1.11 arcs/cy. As for the FK5 and N70E they give nearly zero values. This result is in evident confrontation with an independent determination of the precession constant from LLR and VLBI (Charlot et.al. 1995). If LLR and VLBI results are to be believed, a conclusion follows: in the global sense Hipparcos system is not absolutely independent from the input catalogue (which is FK5-based). Otherwise LLR and VLBI determinations are to be revised. As a result the systems of Hipparcos and N70E (after rigid rotation) should not be considered as rotation free, the systematic difference Δdα in proper motions due to the old precession constant, which is by 0.3 arcs/cy larger than its actual value, can affect the results of secular variation of the longitude of the Sun and produce a linear trend equivalent to the value 0.3 arcs/cy just obtained. If this interpretation is accepted the linear trend should be considered rather as a correction to Fricke's precession Δp1=-0.30 arcs/cy than a drift of the origin of right ascensions with respect to dynamical equinox.
7) Conclusion
An attempt to interpret the complex character of the secular variations of the longitudes was made. The Expanding Spacetime theory presumes violation of the Kepler╣s law and explains the positive quadratic trends in the 20th century. The residual rotation of the Hipparcos based system with respect to dynamical equinox +0.30 arcs ▒0.03 arcs/cy is explained by the fact that Hipparcos proper motion system is not independent from the FK5 system.
References
Charlot, P., Sovers, O. J., Williams, J. G., Newhall, X. X, 1995, AJ, 109, 418
Kolesnik Y. B., 1995, A&A 294, 876
Kolesnik Y. B., 1996, in Feeraz-Mello S., et. al. (eds.) Dynamics, Ephemerids and Astrometry of the Solar System, Kluwer, Dordrecht, p. 477
Kolesnik Y. B., 1997, MNRAS, 285, 1
Masreliez J. 2000, Astroph. Space. Sci. 266, 399
Poppe P. S. R., Leister N., Laclare F., Delmas C., 1999, AJ 116, 2574
Seidelman P. K., Santoro E. J., Pulkkinen K. F. 1985, in Szebenhey V., Balazs B. (eds) Dynamical Astronomy, Austin, Texas, p. 55
Seidelman P. K., Santoro E. J., Pulkkinen K. F. 1986, in Kovalevsky J. and Brumberg V. A.(eds.) Relativity in Celestial Mecanics and Astrometry, Kluwer, Dordrecht, p. 99
Standish E.M., Williams J.G., 1990, in Lieske J.H. and Abalakin V.K. (eds.) Inertial Coordinate System on the Sky , Kluwer, Dordrecht, p.173
Stephenson F. R., Morrison L. V., 1984, Phil. Trans. R. Soc. Lond. A313, 47 Yao Z-G., Smith C., 1988, in Debarbat S., Eddy J.A., Eichhorn H.K., Upgren A.R. (eds.) Mapping the Sky, Kluwer, Dordrecht, p.501
Yao Z-G., Smith C., 1993, in Muller I.I. and Kolaczek B. (eds.) Developments in Astrometry and Their Impact on Astrophysics and Geodynamics, Kluwer, Dordrecht, p.403