Agreement with the supernovae Ia observations and the Surface Brightness test.

1. The EST luminosity relation.

In the SCM there is redshift, popularly (but not quite correctly) explained as a Doppler effect. There is also time dilation, which diminishes the photon arrival rate and further reduces the observed flux. The EST line element may be transformed into a line element of the FRW (Friedmann-Robertson-Walker) type (Masreliez,1999), which models expanding space rather than expanding space and time (scale) and therefore is similar to the SCM line element in that it exhibits both redshift and time dilation. Since all line elements that can be derived via continuous variable transformations are equivalent in General Relativity, the observed luminosity in the EST universe should diminish not only by the redshift, which contributes with a factor 1/(1+z), but there should also be additional cosmological extinction, which contributes by the same factor.

The EST line element is (setting c=1):

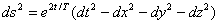
This can be transformed into a FRW line element by:

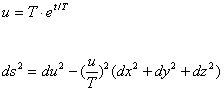
At t=0 and u=T both line elements are Minkowskian and we have dt=du. Since these line elements are physically equivalent the photon arrival rate should be the same and since there is both redshift and time dilation in the FRW line element the same is true in the EST universe.

Another way to see this is to use the transformation:

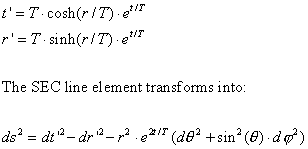
Here r and t in the last term are implicitly defined by the two relations above. In this line element there is neither redshift nor time dilation for radial light propagation, but the received light intensity is diluted inversely proportional to the surface element:

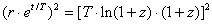
This agrees with the EST luminosity relation (c=1).

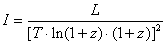
However, the luminosity relation presented in Masreliez 1999, which is the traditional relation for tired light redshift, is incorrect since the second factor 1/(1+z) is missing. Also, since there are two dimming factors 1/(1+z) in the EST model, there is both redshift and time dilation, like in the SCM model.

(Also, relation 12.14 in Masreliez 1999, for the coasting distance traveled by a particle with initial velocity v₀=c· β₀, is not correct; it should be Lr=T·ln(1+z₀), where 1+z₀=[(1+β₀)/(1- β₀)]^½ )

In the EST universe the cosmological scale expansion does not change the average distances between galaxies or their angular sizes, since both space and time expands. 

2. The Supernovae Ia observations.

The EST distance-redshift relation is:

H₀ is the Hubble constant, T the Hubble time and c the speed of light.  According to the EST theory the apparent luminosity expression is:

The corresponding expression for distance in the SCM with flat spacetime is the Mattig distance:

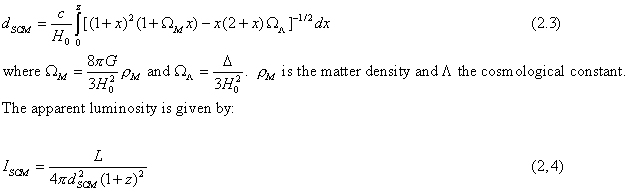
These two expressions for the apparent luminosity agree within 0.03 magnitudes in the range 0<z<1 if Ω_M =0.54 and Ω_Λ=0.46.  The EST luminosity prediction agrees well with the SNe Ia observations as can be seen in Figure 1. It is remarkable that this good agreement with the EST model is obtained without any adjustable parameters (other than the matching at low z-values).

Based on supernovae Ia, CMB temperature anisotropy and galaxy clustering observations the current consensus is that Ω_M =0.3 and Ω_Λ=0.7 (Perlmutter, 2003, Tegmark et. al., 2003).  These are also the values that minimize the least square magnitude difference between the SCM and the EST luminosity relations in the range 0<z<10.0.  The maximum magnitude difference between the two models is now 0.25 dB.

Since the parameters Ω_M and Ω_Λ are selected to make the SCM agree with observations the unexpected dark energy in the SCM might be a consequence of using an inferior cosmological model.  The EST model agrees with observations without adjustment.  However, the EST model implies that the vacuum energy density does not disappear. It is given by the energy-momentum tensor for the EST line element:

Note that Omega equals one by design since T₀₀ is the Critical Density. Furthermore, the net gravitating energy is zero in the EST because the sum of the diagonal elements is zero.

3. The Surface Brightness test.

The Surface Brightness test (Tolman, 1930) uses a test statistic formed by dividing the estimated absolute luminosity L by the estimated surface area of a distant galaxy. The test uses three observational measurements, the apparent luminosity I, the angular size θ and the redshift z. The angular size is used together with an estimated distance, that depends on the redshift and the assumed cosmological model, to estimate the surface area of a galaxy; the area is proportional to (θd)², where d is the distance.

Let the distance when the light was emitted from a test galaxy be d₁ and the distance when the observation is made be d₀. Then for the SCM d₀ =(1+z) d₁, since the distance expands by the factor (1+z) while the light is in transition from the galaxy to the Earth.

Define the surface brightness test statistic, SB, at the time of emission by:

 SB=L/( θ d₁ )²

For the SCM we then have SB = L(1+z) ²/( θ d₀)².

The apparent luminosity is given by:

I=L/[ d₀∙(1+z)]²

This implies SB_SCM= (I/ θ²) (1+z)⁴.

Since both the apparent luminosity and the area depend quadratically on the distance, the test statistic is independent of the particular distance gauge used.

For the EST model the apparent luminosity is also given by:

I= L/[d₀ (1+z)] ²

However, the distance measure d₀ differs between the SCM and the EST models.; Also, distances remain constant during scale expansion d₀ = d₁, for the EST model. We have SB_EST= (I/ θ²) (1+z)² and therefore:

SB_EST /SB_SCM=(1+z)^-2

This shows that the test statistic strongly depends on the model.

Define <SB>=2.5 log(SB)

We get:

<SB_EST> - <SB_SCM>= 2.5∙log (1+z) ^-2= -5.0 ∙log(1+z)

The difference amounts to about 1.4 magnitudes at z=0.9.

The radial distance used in estimating the surface brightness at the time of emission is θ·d₁.

We have for the SCM, with the Mattig distance used by Lubin and Sandage:

And for the EST model:

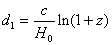
With q₀=0.5 the difference between the logarithms for these two radial distances is about 0.3 dB at z=0.90 (The EST distance is larger).

The open circles in Figure 2 are similar to figure 2, η=2.0, in Lubin and Sandage IV (astro-ph/ 0106566). The filled circles are the corresponding EST estimates.

The estimated local surface brightness for the EST model, arrived at by adjusting the observations by the factor (1+z)², taking into account the difference in radial distance, agrees with the local baseline, but there is significant disagreement with the SCM estimates. Lubin and Sandage IV found this discrepancy to be a factor (1+z)ⁿ, with n in the range 1.19-1.72 in the R-band and 0.45-0.94 in the I-band.

References.

Carroll S.M., Press W.H., Turner E.L., 1992: The Cosmological Constant, Annu. Rev. Astron. Astroph. 30, 499-542

Lubin L. and Sandage A. I, 2001, astro-ph/0102213

Lubin L. and Sandage A. II, 2001, astro-ph/0102214

Lubin L. and Sandage A. III, 2001, astro-ph/0106563

Lubin L. and Sandage A. IV, 2001, astro-ph/0106566

Masreliez C. J., 1999, The Scale Expanding Cosmos Theory, Astroph. & Space Science, 266, Issue 3, p. 399-447

Mattig W.,1958, Astr. Nachr. 284, 109

Tegmark et. al., 2003, astro-ph/0310723

Tolman R. C., 1930, Proc. Nat. Acad. Sci., 16, 511